最近在 Google Reader 中看见科学松鼠会有两篇文章被频繁分享,名为《真理在缩水——现代科学研究方法并不尽善尽美?》(上)与(下),下文简称《缩水》。文章很有意思,而实际上说的是我们的老本行——统计学,因此我在这里也发表一些我的想法和理解,包括这两年我在美帝学习的一些思考,部分内容受益于两位老师 Kaiser 和 Nettleton 教授,先向他们致谢(尽管他们永远都不会看到这篇文章)。同时我也要先说明一下,读这篇文章可能会很花时间(至少我花了大约二十小时写这篇文章),即使我的观点没有价值,我相信里面的引用文献是有价值的。
初读文章,我脑子里冒出的一句话是 “上帝在跟我们掷骰子”,文中给出了大量的不可重复的试验,仿佛就像那些号称 “具有统计学意义”(下文我再说这个所谓的 “意义”)的试验结果只是若干次骰子中的一次运气好的结果而已。读完文章,我们可能不禁要问,到底是真理在缩水,还是它根本就不曾存在?下面我从四个方面来展开,分别说明人对随机性的认识、统计推断的基石、让无数英雄折腰的 P 值、以及可重复的统计研究。
一、感知随机
随机变量在统计分析中占据中心地位,数学上关于随机变量的定义只是一个 “干巴巴的函数”,从样本空间映射到实数集,保证从实数集上的 Borel 域逆回去的集合仍然在原来的 sigma 域中即可。随机变量的性质由其分布函数刻画。写这段话的目的不是为了吓唬你,也不是为了作八股文,而是来说明我为什么不喜欢数学的理由,对我而言,我觉得有些数学工具只是为了让自己不要太心虚,相信某时某刻某个角落有个理论在支撑你,但后果是弱化了人的感知,当然,也有很多数学工具有很强的直觉性(如果可能,我想在未来下一篇文章里面总结这些问题)。我一直认为很多人对随机性的感知是有偏差的,对概率的解释也容易掉进陷阱(参见 Casella & Berger 的 Statistical Inference 第一章,例如条件概率的三囚徒问题)。
《缩水》一文发表了很多不可重复的试验案例,我们应该吃惊吗?我的回答是,未必。举两个简单的例子:
第一个例子:很多数据分析人员都很在意所谓的 “离群点”,论坛上也隔三差五有人问到这样的问题(如何判断和处理离群点),而且也有很多人的做法就是粗暴地删掉,我从来都反对这种做法。除了基于 “数据是宝贵的” 这样简单的想法之外,另一点原因是,离群点也许并非 “异类”。离群点是否真的不容易出现?请打开 R 或其它统计软件,生成 30 个标准正态分布 N(0, 1) 随机数看看结果,比如 R 中输入rnorm(30),这是我运行一次的结果:
> rnorm(30) [1] 1.19062761 -0.85917341 2.90110515 0.59532402 -0.05081508 -0.06814796 [7] 2.08899701 0.76423007 0.92587075 -1.16232929 -0.68074378 -1.40437532 [13] -0.17932604 -0.72980545 -0.53850923 0.21685537 -0.35650714 -1.32591808 [19] -0.88071526 -1.25832441 0.24001498 -0.41682799 -0.09576492 -0.17059052 [25] -0.99947485 0.25108253 -0.47566842 -0.28028786 0.79856649 -0.13250974
30 在现实中是一个比较小的样本量,你看到了什么?2.901?它接近 3 倍标准差的位置了。还有 2.089?…… 如果你不知道这批数据真的是从标准正态分布中生成出来的,现在你会有什么反应?把 2.9 删掉?标准正态分布是一个在我们眼中很 “正常” 的分布,而一个不太大的样本量一次试验足以生成几个“离群点”,那么要是成千上万的试验中没能产生几项震惊世界的结果,你会怎样想?(上帝的骰子坏掉了)
另一个例子和统计学结合紧密一点,我们谈谈残差的 QQ 图。QQ 图是用来检查数据正态性的一种统计图形,与腾讯无关,细节此处略去,大意是图中的点若呈直线状(大致分布在对角线上),那么可以说明数据的正态性比较好,因此 QQ 图经常被用在对回归模型残差的正态性诊断上。我的问题是,即使数据真的是正态分布,你是否真的会看见一些分布在直线上的点?若答案是否定的,那么我们就得重新审视我们对分布和随机的认识了。下图是一幅教科书式的 QQ 图(仍然基于 30 个正态分布随机数):
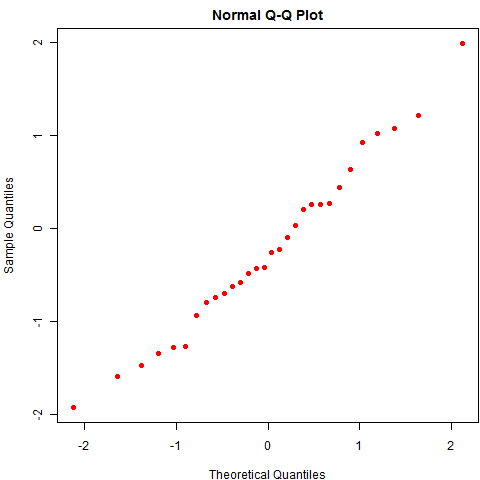
随机性并没有这么美好,即使数据真的来自正态分布,你也有可能很容易观察到歪歪扭扭的 QQ 图,尤其是小样本的情况下。比如下图是 50 次重复抽样的正态数据 QQ 图,它和你想象的 QQ 图本来的样子差多远?
library(animation) set.seed(710) ani.options(interval = 0.1, nmax = 50) par(mar = c(3, 3, 2, 0.5), mgp = c(1.5, 0.5, 0), tcl = -0.3) sim.qqnorm(n = 30, pch = 19, col = "red", last.plot = expression(abline(0, 1)))
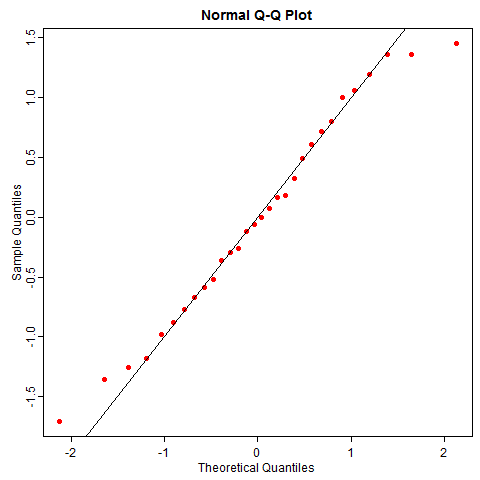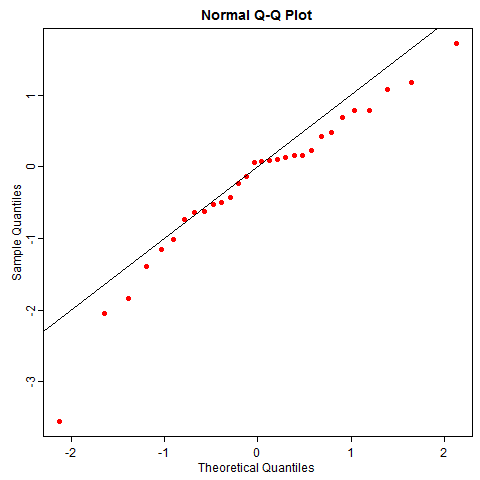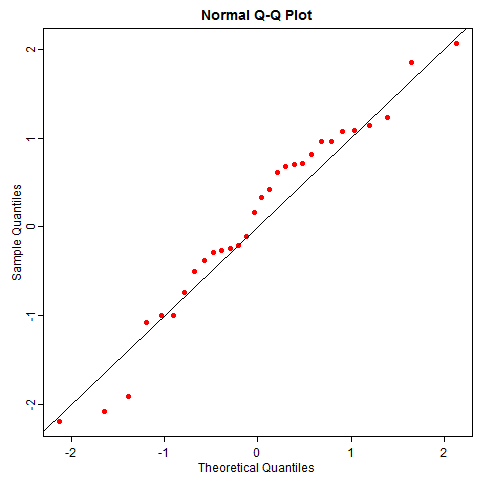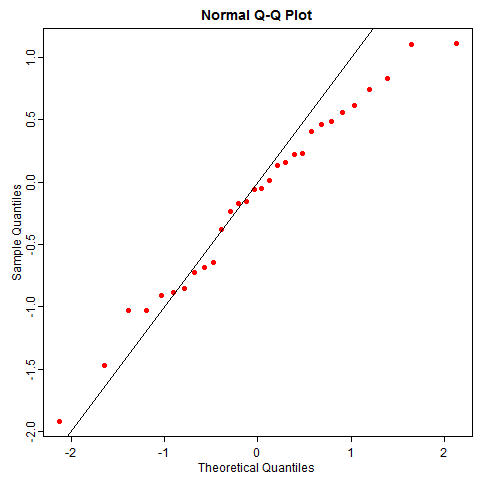
正态分布是统计学中比较 “正常” 的一类分布(台湾学者甚至译为 “常态分布”),我们尚不能很好感知它的随机性,就不必说其它“怪异” 的分布了。
这是我想说的第一点,作为人类,我们对上帝的骰子至少在感知上就可能有问题(别误会,我不信教),接下来从理性角度分析一下。
二、统计推断
《缩水》一文中提到的基本上都是统计推断方法带来的结果,为了理解这些结果,我们必须三思统计推断本身的过程。一般说来,统计推断有两种途径:随机试验和(概率)统计模型,或者说基于试验的推断和基于模型的推断。前者的代表性方法为置换检验(Permutation test),不过它似乎被大多数人遗忘了,更多的人拿到数据首先想的就是用哪个统计模型和分布;实际上,置换检验是一种极具代表性的统计推理方法,可以用典型的 “三段论” 来说明它(参见去年江堂的文章):
- 要么 A,要么 B
- 若有 A,则有 C
- 若非 C,则非 A,于是 B
置换检验的场景是,一次试验中,我们为试验单元随机分配不同的处理(treatment),为了简单起见,假设这里只有两种处理水平 A 和 B,我们想知道两种处理在试验单元的某项指标上是否有显著差异。逻辑是这样:假设处理毫无效果,那么某一个试验对象的指标将不受处理影响,不管我们给老鼠嗑的是 A 药还是 B 药,结果都一样,那么我们可以把处理的标签随机打乱(某些 A、B 随机互换),打乱后 A 组和 B 组的差异不应该会和原来的差异很不一样(因为药不管用嘛),否则,我们恐怕得说,药还是管用的。就这样,我们随机打乱标签很多次,形成一个 “人工生成” 的 AB 差异分布(因为我们生成了很多个差异值),看原来的差异在这个分布的什么位置上,如果在很靠近尾巴的位置上,那么就认为 P 值很小。当了个当,当了个当,P 值出场了。对置换检验熟悉的人是否有想过,好像我们一直没谈到什么分布的假设,那这个概率值(P 值)是从哪里生出来的?答案是最初的“随机分配处理到试验单元上”。这就涉及到试验设计的一大原则:随机化。为什么要随机化?因为试验单元之间可能本来就有差异,换句话说,如果你不随机化,那么你观察到的差异有可能来自试验单元本身。比如,你从笼子里抓前 10 只老鼠给嗑 A 药,后 10 只老鼠给 B 药,这就没有随机化,前 10 只老鼠可能很笨或是老弱病残,容易被你抓住,而后 10 只老鼠跑得贼快。随机化将这些个体差异转变为了随机的误差,例如两只老鼠之间的确本身有差异,但我要是把它们随机分配给处理,那么这种个体差异就会随机进入处理组,保证统计推断有根基。如果这一点没有理解透彻,试验人员很容易在数据收集阶段就已经收集了错误的数据。《缩水》一文中的试验都是怎么做的,我没空去细究。
基于模型的推断的一大特征就是开始对随机变量做一些分布上的假设,例如两样本 t 检验,假设样本来自独立同方差的正态分布。仔细想想这里面的问题,对建模和理解模型结果有至关重要的作用。一个最直接的问题就是,假设条件是否可靠?George Box 大人很久很久以前就说了一句被引用了无数遍的话:所有的模型都是错的,但有些是有用的。统计学方法很 “滑”(用麦兜的话说),它的科学与艺术双重身份,总让人感觉拿捏不准。学数学的人可能觉得艺术太不靠谱,其它外行人士可能觉得科学太神秘。这个问题我不想作答,也无法作答,搁在一边,先说一些我曾经考虑过的问题,它们与《缩水》一文可能并没有直接联系,但应该能或多或少启发我们从源头考虑统计模型,直接上手统计模型的隐患就在于你认为一切都理所当然,随着时间推移,假设渐渐变成了“公理” 和“常识”,我觉得这是很可怕的。
第一个问题是似然函数(likelihood function),它是频率学派的命脉,而我们大多数人仍然都是频率学派的 “教徒”。对于离散变量来说,基于似然函数的方法如极大似然估计很容易理解:我们要找一个参数值,使得观察到的数据发生的概率最大。这里的 “概率” 二字应该被重重划上记号!接下来我要提一个让我曾经觉得后背发凉的问题:
为什么对连续变量来说,似然函数是 ** 密度函数 ** 的乘积?
你是否想过这个问题?我们知道连续变量取任何一个值的概率都是 0,也就是说,如果按照概率的方式解释似然函数,那么连续变量的似然函数应该是 0 才对,换句话说,你观察到的数据发生的概率是 0。现在你觉得似然函数还是一个理所当然的统计工具吗?
有一位统计学家叫 J. K. Lindsey,1998 年在(英国)皇家统计学会宣读了一篇论文,叫 Some statistical heresies(一些统计异端邪说),如果你没见过统计学家打仗,那么这篇论文将会让你看到一场超大规模的战争,后面的讨论者中包括 Murray Aitkin、D. R. Cox 和 J. A. Nelder 等老江湖。Lindsey 的文章几乎是被大家围攻了(期待我这篇文章也能被围攻),不过他对于似然函数的解释倒是让我有点茅塞顿开。细节我不展开,大意是,似然函数也是一种近似(用积分中值定理去想)。
第二个问题是渐近统计(asymptotic statistics),同样,这也是统计学家的日常工具之一,因为太常见,所以也有一种理所当然的味道。比如我们看到列联表就想到卡方检验(检验行列变量的独立性),殊不知卡方检验只是一种大样本下的近似方法。渐近统计的基石是什么?如果你要挖,我想挖到头你一定会挖到泰勒展开。至少目前我认为渐近统计 “基本上就是泰勒展开的第二项(或少数情况下第三项)”。理论上泰勒展开有无穷多项,我们往往根据一些假设条件,把后面的高阶项都消灭掉,剩下一次项或二次项。比如你展开似然函数,就得到了似然比检验的卡方分布;你展开极大似然估计的一个连续函数,你就有了 Delta 方法(当然,需要依分布收敛的前提);就这样左展右展,展出了中心极限定理(对特征函数或母函数展开),展出了拉普拉斯近似(对对数密度函数展开)。如果你能看到这一点,就不会奇怪为什么正态分布在统计推断中有如此中心地位(谁叫正态分布的对数密度函数是个二次函数呢)。
第三个问题是,贝叶斯方法又如何?既然频率学派中几乎处处是近似,贝叶斯学派是否会好一些?我的回答是好不到哪儿去。贝叶斯的逻辑很简单,但由于灵活性太强,应用时非常摧残人的脑力,导致争议不断(先验分布怎么取、MCMC 是否收敛等)。在《缩水》一文中,恐怕是没有基于贝叶斯方法的试验,因为在所谓的科学试验中,人们往往排斥 “先验” 这种想法,就好像先验一定代表主观、而客观一定正确一样。逻辑上,这是荒谬的。关于这些问题的重磅讨论,可参考 Efron 去年发表的 The Future of Indirect Evidence 以及文章后面 Gelman 他们三个人的讨论。我总感觉这不是我这个年龄应该看的东西,太哲学了。
我提到这些问题,本意是给统计学家看的,如果你是一个合格的统计学家,你自己首先应该意识到统计学的局限性,而不是拿到数据就分析。
三、万能的 P 值?
早些年当我还是个无知轻狂小子的时候,我曾戏称 “统计软件就是为了放个 P”,这里的 P 指的是 P 值,不是粗话。这话好像也不全然轻狂无知。使用统计方法的人,难道不是在追逐一个小于 0.05 的 P 值吗?如果你的结果不显著,那么肯定发表不了。换句话说,发表的结果很有可能是我们在自欺欺人。下面的漫画生动刻画了人们寻找 P 值的过程(来自 xkcd):

重大科学发现!吃绿色的软糖会让你长痘痘!95% 置信度!
当你看到 95% 的时候,你看不到红色的、灰色的、褐色的、橙色的、黄色的软糖…… 这便是《缩水》一文中说的 “发表偏见”(publication bias,“偏见” 翻译似乎不妥),即发表的结果是经过人工选择的,你已经不能用正常的概率意义去解读它,或者说,概率已经变了样。
插一句 “统计学意义”:这个概念本来的英文是 statistical significance,但是被很多专业的人翻译为“统计学意义”,我一直认为这很不妥,给人一种错觉,仿佛统计学保证了什么东西有意义一样,我提倡的译法是“统计显著性”。尤其是“由于 P 值小于 0.05,所以具有统计学意义” 这种话,我觉得应该见一句删一句。
上面的软糖问题涉及到传统的多重比较(multiple comparison)与 P 值调整,这里 “传统” 指的是要控制族错误率(Familywise Error Rate,下文简称 FWER)。所谓控制 FWER,也就是要使得一族(多个)统计检验中,一个第一类错误都不犯的概率控制在一定水平之下,比如 0.05。让多个检验全都不犯错和单个检验不犯错(指第一类错误)显然是有区别的,比如假设所有的检验都是独立的,一个检验不犯错的概率是 95%,两个都不犯错的概率就变成了 95% * 95% = 90.25%,检验越多,不犯错的概率就越小。把整体的第一类错误率控制在某个 alpha 值之下,就意味着单个检验必须更 “严格”,因此我们不能再以 0.05 去衡量每个检验是否显著,而要以更小的值去衡量,这就是 P 值的调整,老办法有 Bonferroni 等方法。
控制 FWER 显得有些苛刻,比如有 10000 个基因都需要检验在不同处理下的表达差异,那么要是按照传统的 P 值调整方法,恐怕是很难得出某个基因显著的结论(因为 alpha 值会被调得极其小)。FWER 的目标是一个错误都不能犯,但实际上我们也许可以容忍在那些我们宣称显著的结果中,有少数其实是犯错的,就看你是不是 “宁愿错杀三千,也不放过一个” 了。
Efron 在前面我提到的文章中把 Benjamini 和 Hochberg 在 1995 年的论文称为 “二战以来统计界第二伟大的成果”(他把第一名给了 James & Stein 的有偏估计),那么 B&H 做了什么?答案就是虚假发现率(False Discovery Rate,下文简称 FDR)。FDR 要控制的是在宣称显著的结论中错误的结论的比例,比如 10000 个基因中有 100 个基因显著,但实际上有 5 个是虚假的发现(即本来这 5 个基因分别在两种处理下的表达并没有差异)。尽管有错误存在,但我们认为可以承受。
初学者到这里应该可以意识到了,通过 FDR 选出来的结果在理论上就已经存在错误了,当然这只是小问题,更大的问题在于,FDR 的定义实际上是一个期望的形式:真实的零假设个数除以被拒绝的零假设个数的期望(零假设是没有差异)。凡是涉及到期望的东西,我们都应该冷静三秒想一下,期望意味着什么?
假设有一个游戏,你获胜的概率是 70%,要是赢了,你得到一百万,要是输了,你付出一百万;获利的期望是 40 万。现在我请你去玩,一把定输赢,你玩不玩?我相信大多数人不会玩(除非你实在太有钱了),为什么期望是赚 40 万你也不玩?因为期望往往是 “样本量无穷大” 你才能隐约看到的东西,玩一次游戏,输掉一百万的概率是 30%,恐怕你不敢。
FDR 是个期望,也就是你做很多次试验,平均来看,FDR 在某个数值附近。一次试验中它究竟在哪儿,谁都不知道。就像(频率学派的)置信区间一样,我给你一个区间,其实你并不知道参数在不在区间里,你也无法用概率的方式去描述单个区间,比如你不能说 “参数落在这个区间内的概率是 95%”(只有无数次抽样重新计算区间,这无数个区间覆盖真实参数的概率才是 95%)。
所以,某种意义上,概率论源于赌博,而统计学在骨子里一直都是赌博。旁观者看赌徒,总觉得他在赚钱。当然,统计学家是 “高级赌徒”,他们不是随机乱赌。
四、可重复的统计研究
看到这里,你大概也脑子有点抽筋了(如果你把我提到的 Lindsey 和 Efron 的文章都看过了的话),我们换个轻松点的话题:可重复的统计研究。这不是我第一次提它,我们一直都在号召可重复的统计研究(如《Sweave:打造一个可重复的统计研究流程》)。还是老话一句,不谈道德问题,因为这是不可控的因素,我们可控的只有制度和工具。源代码不会撒谎。
我们期待学术研究过程的透明化,至少统计之都在努力。
关于作者
谢益辉中国人民大学统计硕士,爱荷华州立大学统计学博士,R 包 knitr 的主要作者。现为 RStudio 软件工程师,曾负责 Shiny 包相关开发工作,后转入 R Markdown 相关扩展包的开发,包括 bookdown 和 blogdown。对统计计算、可视化、以及各类网页相关技术感兴趣,有志于对技术写作工具做减法工作,坚信人类浪费了太多时间在期刊论文、学位论文、书籍的排版上。平时主要活跃在 Github 上。个人主页在 https://yihui.name,思想偏激,流水账、意识流甚多,小人之心甚重,慎入。 |
